Example 4: Pendulum Oscillations
The position ( 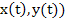 at time at time 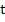 of a particle of mass of a particle of mass 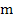 oscillating on a pendulum of length oscillating on a pendulum of length is is
where 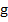 is the acceleration due to gravity, is the acceleration due to gravity, 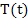 is the tension in the string and is the tension in the string and 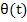 is the angle of the pendulum relative to the vertical at time is the angle of the pendulum relative to the vertical at time 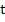 . These equations are however insufficient to guarantee that the particle stays on the string. To ensure that this is so, we must supplement the ODEs by the algebraic constraint. . These equations are however insufficient to guarantee that the particle stays on the string. To ensure that this is so, we must supplement the ODEs by the algebraic constraint.
The two second order differential equations and the constraint comprise a system of three differential algebraic equations (DAE's) for the unknowns 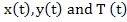 . .
Initial conditions specify 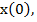 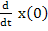 , , 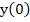 and and 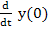 , but not , but not 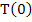 . .
Note: Of course, for this problem, it is easy to eliminate the constraint by introducing the change of variables
This would reduce the DAEs to the second order ODE
IVP's will comprise our initial study and followed by a brief discussion of BVP's.
|