The torus defined above is homeomorphic to
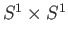 . To see this, let
. To see this, let
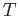 denote the torus and
denote the torus and
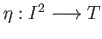 be the quotient map.
Define the map
be the quotient map.
Define the map
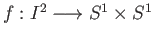 as
as
There is a unique bijection
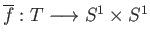 such that
such that
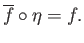 The universal property shows that
The universal property shows that
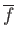 is continuous and since
is continuous and since 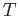 is compact and
is compact and
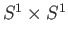 is
Hausdorff, the map
is
Hausdorff, the map
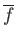 is a closed map and so a homeomorphism.
is a closed map and so a homeomorphism.
nisha
2012-03-20