This is obtained by identifying the opposite sides of the square
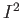 according to the following scheme. For each
according to the following scheme. For each
![$ x \in [0, 1]$](img314.png) , the pair of points
, the pair of points
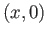 and
and 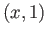 are identified. Likewise for each
are identified. Likewise for each
![$ y \in [0, 1]$](img315.png) the pair of points
the pair of points
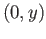 and
and 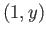 are identified. One first obtains a cylinder
are identified. One first obtains a cylinder
![$ S^1 \times [0, 1]$](img317.png) which is then ``bent around''
and the circular ends are glued together. One obtains a space which looks like the crust of a dough-nut (or medu vada).
which is then ``bent around''
and the circular ends are glued together. One obtains a space which looks like the crust of a dough-nut (or medu vada).
nisha
2012-03-20