Suppose given a planar system of differential equations
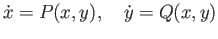 |
(1.1) |
where 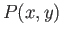 and
and 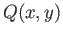 are smooth functions in the plane. Assume that there is an
annulus
are smooth functions in the plane. Assume that there is an
annulus 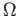 not containing rest points1
and invariant under the flow of the differential equation2. Then
not containing rest points1
and invariant under the flow of the differential equation2. Then
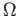 must contain periodic orbits.
must contain periodic orbits.
Figure:
Invariant Annulus
|
[width=.4]GKSBook/fig2/fig2.eps |
The proof of this important result requires the Jordan curve theorem ([8], pp. 52-54).
The analogue of theorem (1.2) is true for differential equations on the sphere but is false for differential equations
on the torus.
The Poincaré Bendixon theorem may be used to prove the existence of limit cycles for the Van der Pol oscillator
by finding an invariant annulus for the flow ([8], pp. 60-61).
Another result from the theory of ordinary differential equations is the following result stated for
planar systems (![[*]](/usr/share/latex2html/icons/crossref.png) ) but holds in higher dimensions also. A proof may be given using
Stokes' theorem or the Brouwer's fixed point theorem (see [8], p. 49).
nisha
2012-03-20
) but holds in higher dimensions also. A proof may be given using
Stokes' theorem or the Brouwer's fixed point theorem (see [8], p. 49).
nisha
2012-03-20