(i) The sphere  is compact and connected and
is compact and connected and
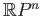 is the continuous image
of
is the continuous image
of  under the projection map
under the projection map 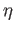 .
.
(ii) Let
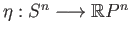 and
and
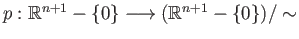 be the projection maps. We have a continuous map
be the projection maps. We have a continuous map
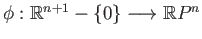 given by the prescription
given by the prescription
where
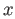 is the
equivalence class of
is the
equivalence class of 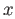 in
in
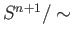 . Denoting by
. Denoting by
![$ [x]$](img295.png) the equivalence class of
the equivalence class of 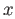 in
in
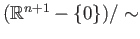 ,
the associated map
,
the associated map
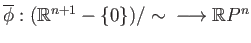 given by
given by
It is readily checked that
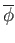 is bijective and
is bijective and
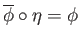 . The universal property now gives us the continuity of
. The universal property now gives us the continuity of
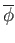 .
Consider now the map
.
Consider now the map
given by
![$ \psi({\bf x}) = [{\bf x}]$](img301.png) which is evidently continuous map. There is a unique map
which is evidently continuous map. There is a unique map
such that
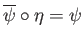 . By the universal property of the quotient we see that
. By the universal property of the quotient we see that
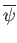 is continuous. It is left as an exercise to check that
is continuous. It is left as an exercise to check that
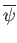 and
and
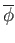 are inverses of each other. Proof of (iii) is left as an exercise.
are inverses of each other. Proof of (iii) is left as an exercise.
We shall see later that the spaces
are Hausdorff as well. The space
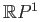 is a familiar space and the proof of the
following result will be left for the reader.
is a familiar space and the proof of the
following result will be left for the reader.
nisha
2012-03-20
![]() and
and
![]() be the projection maps. We have a continuous map
be the projection maps. We have a continuous map
![]() given by the prescription
given by the prescription
![]() is a familiar space and the proof of the
following result will be left for the reader.
is a familiar space and the proof of the
following result will be left for the reader.