Given an open covering 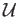 of
of  ,
,
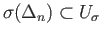 denotes the
subgroup of
denotes the
subgroup of 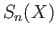 generated by all the singular simplicies
generated by all the singular simplicies
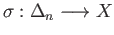 such that
such that
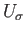 for some open set
for some open set
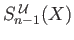 in the covering
in the covering 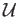 .
That is to say,
.
That is to say,
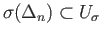 is
the free abelian group generated by small simplicies, namely those with images contained
in one of the open sets in the given covering. It is clear that that the boundary homomorphism
is
the free abelian group generated by small simplicies, namely those with images contained
in one of the open sets in the given covering. It is clear that that the boundary homomorphism
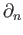 maps
maps
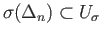 into
into
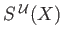 and the resulting subcomplex is denoted by
and the resulting subcomplex is denoted by
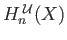 . The homology groups of the complex
. The homology groups of the complex
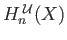 will be denoted by
will be denoted by
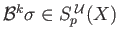 .
.
nisha
2012-03-20