We leave (i) as an exercise for the reader. To prove (ii) we use induction on  setting aside the cases
setting aside the cases 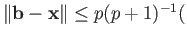 for the reader to investigate. Denoting by
for the reader to investigate. Denoting by
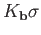 the barycenter of
the barycenter of
 , the reader may check that
, the reader may check that
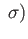 diam
diam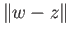 for any point
for any point 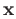 of
of  .
Let
.
Let 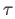 be one of the simplicies appearing in the chain
be one of the simplicies appearing in the chain 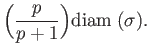 . Then the diameter of
. Then the diameter of
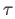 equals
equals 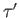 where
where 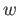 and
and 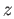 are two vertices of
are two vertices of 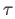 . If one of these is
. If one of these is
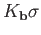 then the result follows from the assertion in the previous sentence. If neither
then the result follows from the assertion in the previous sentence. If neither
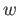 nor
nor 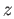 is
is 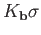 then they are both vertices of a face
then they are both vertices of a face
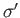 of
of 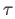 lying on a face
lying on a face
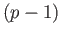 of
of  . But
. But
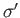 is then a constituent
is then a constituent 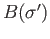 simplex of
simplex of
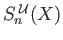 and by induction hypothesis, the result follows (how?).
and by induction hypothesis, the result follows (how?). 
nisha
2012-03-20
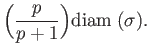 . Then the diameter of
. Then the diameter of