(i) The barycenter of a zero simplex, that is a point, is the zero simplex itself.
(ii) The barycenter of an affine  -simplex
-simplex
![$ [{\bf v}_1, {\bf v}_2,\dots, {\bf v}_{p+1}]$](img2591.png) is the point
is the point
The barycenter of a one simplex is its midpoint and the barycenter of a two simplex is the
centroid of the triangle determined by the vertices. Roughly speaking,
the barycentric subdivision of a one simplex is obtained by subdividing the segment at its midpoint, or equivalently
constructing the cone of each of the two endpoints with apex as the barycenter.
To subdivide a two simplex, we first subdivide each of its three sides resulting in six one simplicies
and taking the cone of each of the six pieces
with apex as the barycenter of the two simplex. Figure below depicts these subdivisions.
in
More precisely the result of subdividing an affine 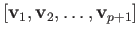 simplex is a
simplex is a 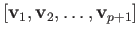 chain. The rough description above
suggests an inductive definition.
chain. The rough description above
suggests an inductive definition.
nisha
2012-03-20
![]() -simplex
-simplex
![]() is the point
is the point