Given a singular 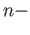 simplex
simplex
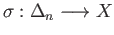 , its
, its 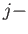 th singular boundary is the singular
th singular boundary is the singular 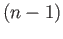 simplex
simplex
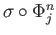 and the boundary
and the boundary
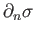 of
of 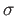 is then the
is then the 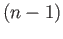 chain given by the algebraic sum of its singular faces:
chain given by the algebraic sum of its singular faces:
The map
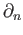 then extends as a group homomorphism
then extends as a group homomorphism
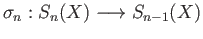 . When
. When 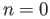 we
define the boundary map
we
define the boundary map
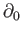 to be the zero map.
to be the zero map.
The most important property of the maps
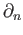 is the vanishing of
is the vanishing of
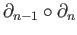 which we now prove.
which we now prove.
nisha
2012-03-20
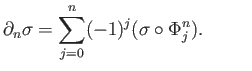
![]() is the vanishing of
is the vanishing of
![]() which we now prove.
which we now prove.