Denote the adjoined points in
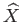 and
and
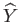 as
as  and
and 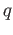 respectively and extend the given map by
sending
respectively and extend the given map by
sending  to
to 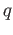 . We need to show that the extension is continuous at
. We need to show that the extension is continuous at  .
Let
.
Let 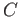 be any compact subset of
be any compact subset of  so that
so that
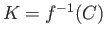 is compact in
is compact in  . Then
. Then
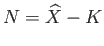 is a neighborhood of
is a neighborhood of  in
in
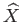 that is mapped by
that is mapped by
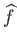 into the preassigned neighborhood
into the preassigned neighborhood
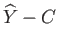 of
of 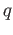 . This proves the
continuity of the extension.
. This proves the
continuity of the extension.
The converse is not true as the constant map shows. However the following version in the reverse
direction is easy to see,
nisha
2012-03-20