Now remember that individuals of any generation may reproduce without depending on any other individual of any previous generations or any one of the same generation.
Thus we have 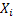 as the random variable (r.v) which denotes the offspring of an individual and as the random variable (r.v) which denotes the offspring of an individual and 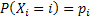 , , 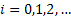 , such that , such that 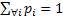 and and 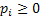 hold true. Here hold true. Here 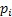 is the offspring distribution of an individual and it is generally denoted by is the offspring distribution of an individual and it is generally denoted by  . This process can be considered a simple example of Markov Chain and we are interested in the distribution of the nth generation size. . This process can be considered a simple example of Markov Chain and we are interested in the distribution of the nth generation size.
Also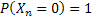 , would simply imply the extinction of the species at any nth generation, and also remember , would simply imply the extinction of the species at any nth generation, and also remember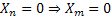 , , 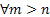 . .
To start the process we assume 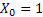 and and  and and  as the mean and the variance of the off spring distribution, i.e., of as the mean and the variance of the off spring distribution, i.e., of  assuming assuming .Then: .Then: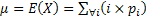 and and 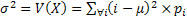 holds true. holds true.
With 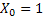 , the following diagram (Figure 3.1) will illustrate the branching process more clearly , the following diagram (Figure 3.1) will illustrate the branching process more clearly
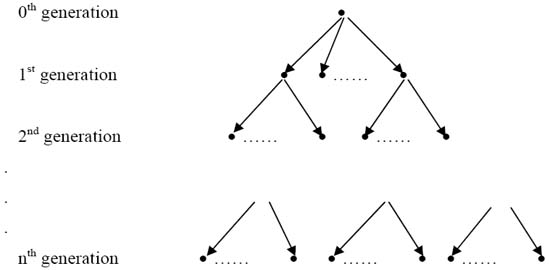 |
Figure 3.1: A typical example of branching process |
|