Branching process
Let us consider a population such that it consists of individuals which produce off springs of the same kind in the next generation and this continues from generation to generation. If an individual produces 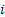 number of off springs, then number of off springs, then 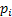 is the corresponding probability, and this probability is independent of how the other reproduces or propagate. For illustration let us consider the growth of bacteria or amoeba, where for simplicity we assume the following: is the corresponding probability, and this probability is independent of how the other reproduces or propagate. For illustration let us consider the growth of bacteria or amoeba, where for simplicity we assume the following:
Step 1: 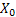 : The zeroth generation, i.e., from where we begin the whole process and let us term this as the ancestor. : The zeroth generation, i.e., from where we begin the whole process and let us term this as the ancestor.
Step 2: 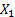 : Off spring of : Off spring of 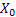 and is called the first generation (wrt to and is called the first generation (wrt to 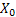 ). ).
Step 3: 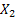 : Off spring of : Off spring of 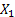 and is called the second generation (wrt to and is called the second generation (wrt to 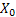 ). ).
Step 4:………
.
.
.
Step 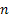 : : 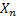 : Offspring of : Offspring of 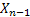 and called the and called the 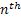 generation (wrt to generation (wrt to 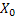 ). ).
|