| |
If 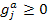 indicates indicates 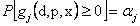 , then it means that the constraint is feasible. With this inverse reliability transformation, the original constraints that require reliability assessments are converted to equivalent constraints that evaluate the αj-percentile performance. Hence instead of checking the actual reliability, the location of , then it means that the constraint is feasible. With this inverse reliability transformation, the original constraints that require reliability assessments are converted to equivalent constraints that evaluate the αj-percentile performance. Hence instead of checking the actual reliability, the location of 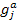 will now determine the feasibility of a constraint. Applying the above concept to a portfolio optimization (considering minimization) problem gives us the following two equations, namely (12.4) and (12.5). will now determine the feasibility of a constraint. Applying the above concept to a portfolio optimization (considering minimization) problem gives us the following two equations, namely (12.4) and (12.5).
Here the deterministic portfolio optimization problem, (12.4), and the reliable formulation, (12.5), correspond to the general equations (12.2) and (12.3) respectively. N is the universe of assets from which the portfolio is to be formed, Ω, the vector comprising the weights 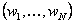 for each of the corresponding asset in the optimal portfolio, M, the vector consisting of the expected returns for the N assets and finally, V, the variance-covariance matrix of the returns of the N assets. In (12.5) the constraint on the returns means that the probability of returns being greater than a certain desired value R* satisfies a given confidence level for each of the corresponding asset in the optimal portfolio, M, the vector consisting of the expected returns for the N assets and finally, V, the variance-covariance matrix of the returns of the N assets. In (12.5) the constraint on the returns means that the probability of returns being greater than a certain desired value R* satisfies a given confidence level 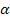 . .
|