The concept illustrated with this simple two tree diagram is denoted by the binomial tree concept (Figure 18), and in case there are more than two such outcomes we have the multi-nomial tree concept as shown below through Figure 19.
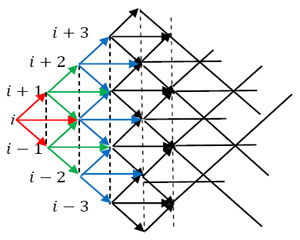
Figure: 10.9: Multinomial (for three) tree concept extended for more than one stage and more than one state
Now consider that we are interested to form a hedged portfolio where the portfolio is a stock and a claim, hence the portfolio value can either increase or decrease by a certain value as depicted in the diagram below (Figure 20)
Figure 10.10: A combination of a stock and a claim
Here  is a fixed number and the portfolio as we can see consists of (i) one stock and (ii) one claim. is a fixed number and the portfolio as we can see consists of (i) one stock and (ii) one claim.
Now our task it to choose the value of  (say (say 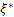 ) such that the pay offs are same in each state, which means that ) such that the pay offs are same in each state, which means that
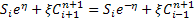 , from which we have: , from which we have: 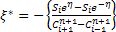
Thus we have created a risk free portfolio or investment to avoid any arbitrage opportunity. Now one should remember that this investment or portfolio should grow at the risk free interest rate, 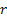 , else the opportunity of making extra-ordinary profit is evident. , else the opportunity of making extra-ordinary profit is evident.
|