| |
Rule 8.3
The expected due date (EDD) rule minimizes the maximum lateness for arbitrary distributed processing times and deterministic due dates in the class of nonpreemptive static list policies, the class of nonpreemptive dynamic policies, and the class of preemptive dynamic policies.
Rule 8.4
The policy that maximizes the total discounted expected reward in the class of preemptive dynamic policies prescribed, at each point in time, is found out using the value of largest Gittin's index, where Gittin's index is given by the formulae, 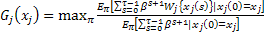 , where , where 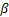 is the discounted factor between 0 and 1. is the discounted factor between 0 and 1.
Example 8.2 for rule 8.4
Consider we have 3 jobs marked as 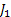 , , 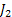 and and 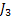 . Let the corresponding weights of the 3 jobs be . Let the corresponding weights of the 3 jobs be 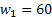 , , 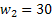 and and 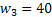 . For simplicity let us assume that the processing times of the 3 jobs can only be integer values and those values are 1, 2 and 3. Moreover the corresponding probabilities for the 3 jobs are as follows : . For simplicity let us assume that the processing times of the 3 jobs can only be integer values and those values are 1, 2 and 3. Moreover the corresponding probabilities for the 3 jobs are as follows :
- Job
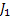 : : 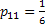 , , 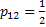 and and 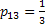
- Job
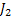 : : 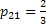 , , 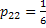 and and 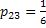
- Job
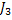 : : 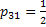 , , 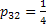 and and 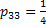
Let us assume the value of 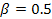 . Now the next step is to find the value of Gittin's index for each job and they are calculated as follows . Now the next step is to find the value of Gittin's index for each job and they are calculated as follows |