| |
Some scheduling rules
Rule 8.1
It is easy to find the optimal permutation schedule for the stochastic counterpart of 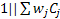 , when the processing time of job , when the processing time of job 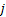 is is 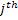 and that is from an arbitrary distribution and that is from an arbitrary distribution 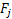 and the objective is and the objective is 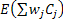 . This leads to the concept of weighted shortest expected processing time (WSEPT), under which one sequences the jobs in decreasing order of the ratio . This leads to the concept of weighted shortest expected processing time (WSEPT), under which one sequences the jobs in decreasing order of the ratio 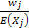 or or 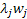 . It can be proved that WSEPT rule minimizes the expected sum of the weighted completion times in the class of nonpreemptive static list policies as well as in the class of nonpreemptive dynamic policies. . It can be proved that WSEPT rule minimizes the expected sum of the weighted completion times in the class of nonpreemptive static list policies as well as in the class of nonpreemptive dynamic policies.
Rule 8.2
Let us consider the stochastic version of 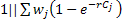 , where , where 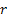 is the discounted factor, with arbitrary processing times. Thus it leads us to the concept of weighted discounted shortest processing time first (WDESPT), under which one can minimize the expected weighted sum of the discounted completion times in the class of nonpreemptive static list policies as well as in the class of nonpreemptive dynamic policies. is the discounted factor, with arbitrary processing times. Thus it leads us to the concept of weighted discounted shortest processing time first (WDESPT), under which one can minimize the expected weighted sum of the discounted completion times in the class of nonpreemptive static list policies as well as in the class of nonpreemptive dynamic policies.
Example 8.1 for rule 8.2
Let us take a simple example where there are 3 jobs with priority 1,2 and 3. Furthermore the processing time distribution of the 3 jobs namely 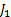 , , 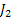 and and 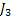 is is 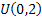 , , 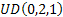 and and 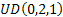 respectively. Given this information we can easily find that respectively. Given this information we can easily find that 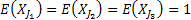 , thus , thus 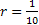 . Furthermore the priority indices of the jobs are calculated as follows: . Furthermore the priority indices of the jobs are calculated as follows:
- Job # 1, i.e.,:
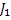 : : 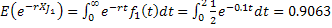
- Job # 2, i.e.,:
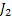 : : 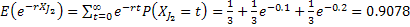
- Job # 3, i.e.,:
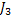 : : 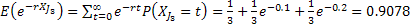
Thus the priority indices are: 9.678, 9.852 and 9.852, so once can either schedule 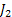 or or 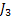 first and then first and then 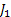 In order to make a judicious decision between In order to make a judicious decision between 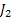 and and 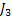 , one needs to find the variance and schedule the one which has larger variance, and here is where the concept of stochastic dominance with respect to expected value as well variance comes into the picture.. , one needs to find the variance and schedule the one which has larger variance, and here is where the concept of stochastic dominance with respect to expected value as well variance comes into the picture.. |