| |
Example 7.9
(a) Consider a single queue model where only one customer is allowed in the system. If another customer comes and finds the queue busy then he/she goes away and never returns, while is the queue is empty he/she approaches the server and is served. Assume the arrival distribution is Poisson with mean value of 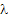 per unit time and the service time is Exponential with a mean value of per unit time and the service time is Exponential with a mean value of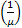 time units. With this information time units. With this information
(i) Set up the transition diagram and determine the balance equations.
(ii) Determine the steady state probabilities.
(iii) Determine the average number in the system.
(b) Can you solve the same set of three (3) question as asked for Assignment # 3 (above) for the case when only two (2) customers are allowed in the sytem.
Specialized Poisson Queues
Here we have one (1) queue and 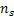 number of servers, i.e., a good look at the diagram below will illustrate the set up very clearly. number of servers, i.e., a good look at the diagram below will illustrate the set up very clearly.
Thus we have the 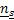 number of server system, but only with one (1) queue having number of server system, but only with one (1) queue having 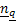 number of people in the queue at any point of time. The arrival rate number of people in the queue at any point of time. The arrival rate 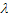 is the number of customers per unit time which is constant for the whole system, while the service rate for the different servers are is the number of customers per unit time which is constant for the whole system, while the service rate for the different servers are 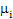 , ,
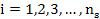 . For simplicity we consider they are the same, i.e., . For simplicity we consider they are the same, i.e., 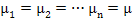 . One should be aware that we make a distinction between the system and the queue, where the former implies the whole set up as such, while queue is the part of the system from where people/machines are being sent to the servers for the processing operation . One should be aware that we make a distinction between the system and the queue, where the former implies the whole set up as such, while queue is the part of the system from where people/machines are being sent to the servers for the processing operation
|