| |
Few more example of Markov chain
Example 1.24
Suppose customers arrive at a service station/centre in a 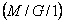 queue system in accordance with Poisson process with an average rate of queue system in accordance with Poisson process with an average rate of 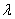 . As this is a single server, thus when customers arrive, if they find the server in not being used they immediately go to the server and their respective job is processes, else if the server is busy the customers wait. We are to plan out scheduling system in such a way that we optimize on the metric which we consider as important to analyze how the queueing system works. Some of the metric may be average waiting time for the jobs, average idle time of the server, average processing time of the jobs, etc. . As this is a single server, thus when customers arrive, if they find the server in not being used they immediately go to the server and their respective job is processes, else if the server is busy the customers wait. We are to plan out scheduling system in such a way that we optimize on the metric which we consider as important to analyze how the queueing system works. Some of the metric may be average waiting time for the jobs, average idle time of the server, average processing time of the jobs, etc.
Example 1.25
In this second example consider you have 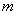 number of serves, such that that the queueing system is now denoted by number of serves, such that that the queueing system is now denoted by 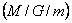 . Further more, consider that all the servers are machines which are particular types of machines like shaper, planner, grinder, etc., such that each is capable of performing only one operation. All the jobs are required to be machined by all of these . Further more, consider that all the servers are machines which are particular types of machines like shaper, planner, grinder, etc., such that each is capable of performing only one operation. All the jobs are required to be machined by all of these 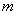 servers/machines, but in any order. The arrival rate of the jobs is a Poisson process with an average rate of servers/machines, but in any order. The arrival rate of the jobs is a Poisson process with an average rate of 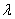 , and the throughput of the servers/machines are , and the throughput of the servers/machines are 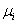 , , 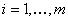 . As evident from the first example stated above, our plan for scheduling this queueing system can be based in a way that we optimize on the metric which we consider as important to analyze how the queueing system works. Some of the metric may be average waiting time for all the jobs, average idle time of all the servers/machines, average processing time of all the jobs, ratio of average utilization between the most used server/machine with respect to least used server/machine, etc. . As evident from the first example stated above, our plan for scheduling this queueing system can be based in a way that we optimize on the metric which we consider as important to analyze how the queueing system works. Some of the metric may be average waiting time for all the jobs, average idle time of all the servers/machines, average processing time of all the jobs, ratio of average utilization between the most used server/machine with respect to least used server/machine, etc.
Without any loss of generality let us discuss again the limit theorems for Markov chains |