| |
Theorem 1.4
Suppose  , ,  and and 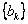 be three sequences indexed by be three sequences indexed by 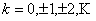 . Also suppose the following are true: (i) . Also suppose the following are true: (i) 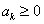 , (ii) , (ii) 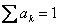 , (iii) , (iii) 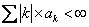 , (iv) , (iv) 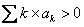 , (v) , (v) 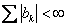 , and that the greatest common divisor of the integer , and that the greatest common divisor of the integer 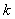 for which for which 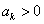 is 1. is 1.
Proof of Theorem 1.4
(a) If the renewal equation 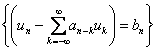 for for 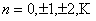 is satisfied by a bounded sequence is satisfied by a bounded sequence  of real numbers, then (i) of real numbers, then (i) 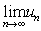 and (ii) and (ii) 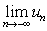 exist. exist.
(b) Furthermore if 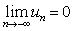 (i.e., (ii)) then (i.e., (ii)) then 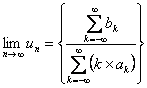 [Note in case the denominator is equal to infinity, i.e., [Note in case the denominator is equal to infinity, i.e.,  , then the limit is still valid provided we can interpret or say that , then the limit is still valid provided we can interpret or say that
Now before going into the proof we will give the general definition of a renewal process where the equation would be of the form 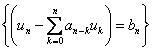 for for 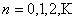 . So consider a light bulb whose lifetime (obviously will be measured in discrete times) is a random variable, . So consider a light bulb whose lifetime (obviously will be measured in discrete times) is a random variable, 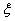 , where , where 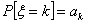 for for 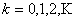 , , 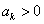 , , 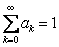 . Now if each bulb is replaced by a new one the moment the old bulb fails (fuses), such that first bulb lasts until . Now if each bulb is replaced by a new one the moment the old bulb fails (fuses), such that first bulb lasts until 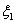 time, the second bulb lasts until time, the second bulb lasts until 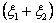 time and so on and we must remember that time and so on and we must remember that 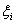 are each i.i.d. Let are each i.i.d. Let 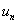 denote the expected number of renewals (replacements) up to time denote the expected number of renewals (replacements) up to time 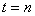 . So the first replacement occurs at time . So the first replacement occurs at time 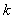 , then the expected number of replacements in the remaining time upto to , then the expected number of replacements in the remaining time upto to 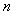 is is 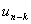 and summing over all possible values of and summing over all possible values of 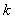 we have we have
Now remember the first term, 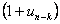 is the expected number of bulbs replaced in time is the expected number of bulbs replaced in time 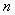 if the first bulb fails at time if the first bulb fails at time 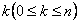 , and the probability of this event is , and the probability of this event is 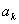 , while the second sum is the sum of the probability that the first bulb lasts a duration exceeding , while the second sum is the sum of the probability that the first bulb lasts a duration exceeding 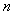 time units. time units. |