| |
Wiener Process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener, and this process is also called the standard Brownian motion, after Robert Brown. It is one of the best known Lévy processes (stochastic processes with stationary independent increments) and is quite frequently used in in pure and applied mathematics, economics, physics, finance, etc.
Let us characterize the Wiener process, 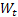 , as given below , as given below
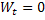 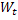 has independent increments such that has independent increments such that 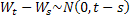 , where , where 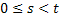
The basic properties of the Wiener process are as follows :
The unconditional probability density function at a fixed time  is given by is given by 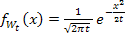 , such that we can easily prove that the following holds. , such that we can easily prove that the following holds.
|