For an ease of understanding let is refer to Figure 6.9, which illustrates the random movement of a particle inside a chamber. The movement of the particle A happens as shown by the arrow.
Let the partile start at 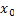 and suppose it makes and suppose it makes 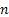 steps. Let us also define the following steps. Let us also define the following
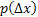 = Probability that the particle moves a distance = Probability that the particle moves a distance 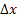 which is independent of either which is independent of either 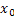 or or 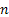
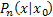 = Probability that the particle is at = Probability that the particle is at 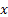 (which is a vector of dimension (which is a vector of dimension 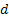 ) )
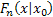 = Probability that the particle is at = Probability that the particle is at 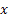 for the first time for the first time
Thus we can show that 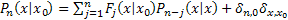 . Now to solve . Now to solve 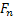 we introduce the generating function and apply the discrete version of the convolution theorem. we introduce the generating function and apply the discrete version of the convolution theorem.
Thus we have:
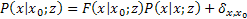 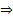 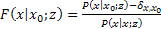
Now inverting the trsansform and using Taylor series expansion we get 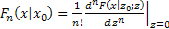
We can also find the eventualprobability that the particle returns to its original place from where it started and that is already calculated by us.
|