| |
Consider the problem called the Gambler's ruin, where the gambler starts with Rs. X and at each play of the game he/she wins Rs. 1 or losses Rs. 1. Once the gambler reaches the state where he/she losses all the money then he/she continues to stay at that level where his/her money is Rs. 0. Hence if we follow these assumptions then we should have 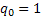 , , 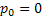 . Moreover . Moreover 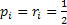 , while , while 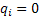 , , 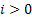 . This provides us with the information such that one can easily draw the transition probability matrix as . This provides us with the information such that one can easily draw the transition probability matrix as 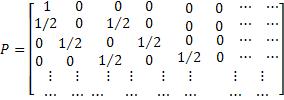 . Now holding the time tighter and tighter we can have this process converge to the Brownian moton. As a remark we would like to mention that the relationship between convergence of the above model to the Brownian motion and that of binomial model to Black Schole's model (in finance) is quite interesting. Based on this we can work on a simple problem, where if we start with Rs. 100 then we can easily say that the answer to the question that we will eventually ruin with certainty is a yes and the answer to how long it will take to do that is infinity. . Now holding the time tighter and tighter we can have this process converge to the Brownian moton. As a remark we would like to mention that the relationship between convergence of the above model to the Brownian motion and that of binomial model to Black Schole's model (in finance) is quite interesting. Based on this we can work on a simple problem, where if we start with Rs. 100 then we can easily say that the answer to the question that we will eventually ruin with certainty is a yes and the answer to how long it will take to do that is infinity. |