| |
Random Walk
As already discussed there is another type of Markov chain using which we model the behaviour of a particle experiencing a random nature of movement, such that if the particle is in state 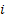 then we assume that it can either move up, i.e., go to state then we assume that it can either move up, i.e., go to state 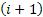 or stay at the same position, which is or stay at the same position, which is 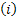 or move down to or move down to 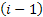 during the next period (which is one unit). We may denote the movements with the probabilities (i) during the next period (which is one unit). We may denote the movements with the probabilities (i) 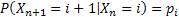 ; (ii) ; (ii) 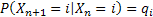 and (iii) and (iii) 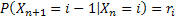 ), where ), where 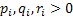 and and 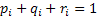 . Thus the transition matrix would be denoted by . Thus the transition matrix would be denoted by 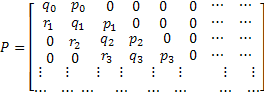 , which as we know is a sparse matrix or more precisely as the tri-diagonal matrix. We can consider examples where (i) , which as we know is a sparse matrix or more precisely as the tri-diagonal matrix. We can consider examples where (i) 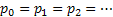 , , 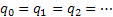 and and 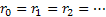 or (ii) or (ii) 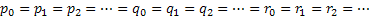 hold true such that the transition matrix will be modified accordingly. hold true such that the transition matrix will be modified accordingly.
|