Theorem 4.5 (Wald's Equations)
Consider a sequence 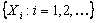 which are i.i.d, have a finite expectation and also assume that which are i.i.d, have a finite expectation and also assume that 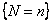 is a stopping time for is a stopping time for 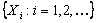 , such that , such that 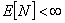 , then , then
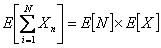 . .
Proof of Theorem 4.5
Before we venture in trying to proof the above theorem note the interesting thing when both 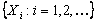 and and 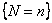 are probabilistic. are probabilistic.
Let us consider the indicator function, 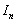 , where , where 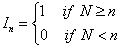 , such that we will have , such that we will have
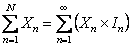 . .
Hence
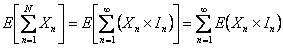
We will stop if we successfully observe  . Thus we do not terminate our experiment as and when we like but continue to observe and stop ONLY at the last reading which is . Thus we do not terminate our experiment as and when we like but continue to observe and stop ONLY at the last reading which is 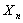 . Therefore . Therefore 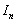 is independent of is independent of 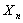 . .
We thus obtain
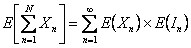
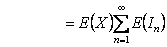 (remember here the suffix (remember here the suffix 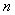 is not relevant as it can be any is not relevant as it can be any 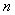 ) )
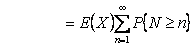
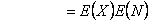
Let 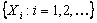 denote the inter arrival time of a renewal process. In this experiment let us consider we stop at the first renewal after denote the inter arrival time of a renewal process. In this experiment let us consider we stop at the first renewal after 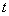 , i.e., at the , i.e., at the 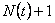 renewal. renewal.
Note
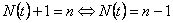
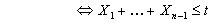 and and 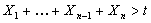
Thus the event 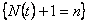 depends only on depends only on 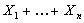 and is definitely independent of and is definitely independent of 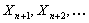 such that such that 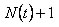 is the stopping time is the stopping time
|