Wald's equation
An integer valued random variable (r.v) is said to be a stopping time for a sequence 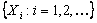 if the if the
event 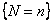 is independent of is independent of 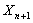 , , 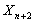 ,… for all ,… for all 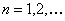 . Thus one would observe . Thus one would observe 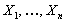 in a sequential order where in a sequential order where 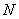 (remember it is a random variable (r.v)) denotes the number observed before one stops. Thus if (remember it is a random variable (r.v)) denotes the number observed before one stops. Thus if 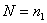 , then we have observed , then we have observed 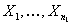 and not observed and not observed 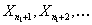
Let us illustrate this concept of stopping time with an example.
Example 4.5
Consider 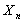 , , 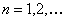 be independent such that be independent such that 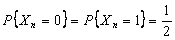 , , 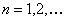 .Assume that we have .Assume that we have 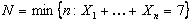 , then this , then this 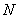 is a stopping time. Example can be when we keeping flipping an unbiased coin and stop the experiment the moment the number of tails is 7. is a stopping time. Example can be when we keeping flipping an unbiased coin and stop the experiment the moment the number of tails is 7.
|