Note
- For large values of
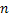 , , 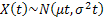
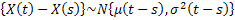
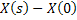 and and 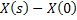 are mutually independent, which implies are mutually independent, which implies 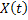 is a Markov process is a Markov process
Thus we say a stochastic process is Weiner-Einsten process (Figure 3.2) with drift parameter 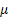 and variance parameter and variance parameter 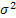 if if
1. For disjoint intervals 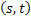 and and 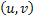 where where 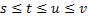 , , 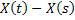 and and 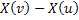 are independent and this implies it is Markov process with independent increments (Figure 3.2). are independent and this implies it is Markov process with independent increments (Figure 3.2).
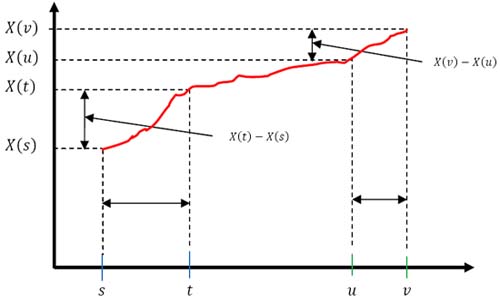 |
Figure 3.2: Illustration of Weiner-Einsten process to show that it has independent increments |
2. 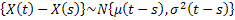 and this implies it is Gaussian. and this implies it is Gaussian.
3. Since # 2 above is true hence the transition probability density function is given by
|