| |
Weiner process
Consider a particle which is undergoing Brownian motion performes a random walk such that as time changes from 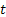 to to 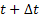 , the position of the particle also changes from , the position of the particle also changes from 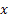 to to 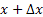 . One should be aware that the total displacement of the particle in time . One should be aware that the total displacement of the particle in time 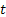 is is 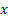 . Also suppose that the random variable . Also suppose that the random variable 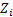 denotes the length of the denotes the length of the 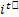 step taken by the particle in the time interval of step taken by the particle in the time interval of 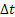 , such that , such that 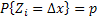 and and 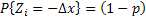 and and 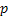 is independent of both is independent of both 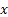 and and 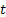 . .
Now these 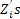 are i.i.d. and assume you divide the interval length into are i.i.d. and assume you divide the interval length into 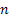 equal subintervals each of length equal subintervals each of length 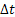 , such that , such that 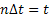 . The total displacement . The total displacement 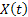 is given by is given by 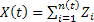
Hence:
Now assume as 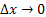 , , 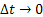 then then
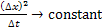 and and 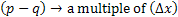 |
(3.6) |
Moreover consider
If (3.6), (3.7) and (3.8) are true it would mean that
|