| |
Note
In financial time series (specially stock prices) either the 1st, 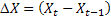 or the 2nd, or the 2nd,  , differences generally produce stationary time series, which in many cases lead to the fact that the changes are i.i.d. In time series we can utilize many of the techniques like GARCH, A-GARCH, E-GARCH, PC-GARCH, etc., to first find whether the series are in a sense i.i.d. In that case one should then utilize the fact that given the mean and variance of the first stage what are the subsequent mean and variances values. , differences generally produce stationary time series, which in many cases lead to the fact that the changes are i.i.d. In time series we can utilize many of the techniques like GARCH, A-GARCH, E-GARCH, PC-GARCH, etc., to first find whether the series are in a sense i.i.d. In that case one should then utilize the fact that given the mean and variance of the first stage what are the subsequent mean and variances values.
Now let us take this example one step further, where 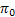 denotes the probability that starting with only one individual the population dies out, i.e., denotes the probability that starting with only one individual the population dies out, i.e.,  , so that we have , so that we have 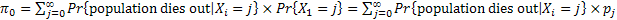 . .
Logically the whole population will eventually die iff each of the families started by the members of the first generation eventually die (as we assume that generation of each member are being reproduced independently), hence we will obtain  (which is true as the concept of independence holds true). (which is true as the concept of independence holds true).
Note
The probability of ultimate extinction of the branching process means  , thus , thus  implies that implies that  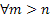 . . |