| |
Definition
Consider 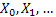 are the random variables that denote the size of the 0th generation, 1st generation, etc respectively, Figure 3.1. Also assume that an individual in any generation produce are the random variables that denote the size of the 0th generation, 1st generation, etc respectively, Figure 3.1. Also assume that an individual in any generation produce 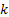 number of off-springs and the probability be number of off-springs and the probability be 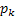 , , 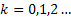 . It is quite simple to note that . It is quite simple to note that 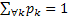 . Then the sequence, . Then the sequence, 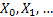 , i.e., , i.e., 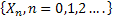 is the Galton Watson branching process. is the Galton Watson branching process.
In the Galton Watson branching process let us assume 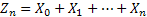 , where as per definition , where as per definition 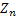 is the total number of progeny upto to the is the total number of progeny upto to the 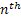 generation. generation.
Then:
|