The sentence, 'The grass is green' is true because it corresponds to the object called grass whose colour is green. A question is raised here, "Can meaning be purely defined in truth conditional terms?" In order to resolve this problem, Frege makes a distinction between 'sense' and 'reference'. The analysis of this distinction between sense and reference is based on the puzzle between identity statements.

The term 'identity' is first of all a relation. It is a relation between things, and further, the minimum requirement of the relation is that at least it must be holding between the two. Suppose, A and B are two different expressions. The identity relation between A and B states that "A coincides with B" or "A is similar with B". Let us take an example.

1. A = A
2. A = B

In the first case, we are not getting any new information, because it is just the repetition, whereas in the second case, we are getting some new information based on the cognitive value of the expressions.

Let us take a look at the famous example cited by Frege;

1. The morning star is same as morning star.
2. The morning star is same as evening star.

The first proposition states that 'the morning star' is identical with 'the morning star' and it is known by the principle of analyticity and synonimity. So, it is true by virtue of its definition. On the other hand, the second proposition gives us the information that 'the morning star' is same as 'the evening star'. This identity is derived from the empirical discovery. This sentence is true by virtue of our experience. Both the above propositions are true. However it is noticed that these two propositions differ in their meaning but not with their reference, since they refer to the same object called 'Venus'. A question is raised here, i.e., if meaning of the two propositions differ then how can we claim that they are identical with each other. Frege answers that sentences possess meaning when their constituent parts are having a specific meaning and they correspond to the specific object. This analysis is found in his 'compositionality theory of meaning'. Further, he states that meaning of an expression is unchanged if we substitute one expression with other which has the same reference.

Frege has taken three arguments for explaining the identity relation. The identity relation holds between the;

1. Objects
2. Names
3. Signs of objects

Considering the third issue, he states that 'signs' are not arbitrary. It has a definite sense. The difference between two signs can arise when their mode of presentation differs from each other. For example,²

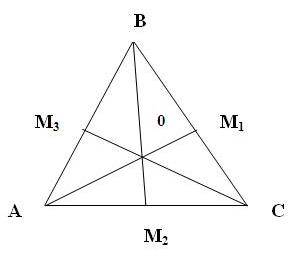
In this triangle, the point of the intersection between 'A' and 'B' is the referring expression and the expressions 'M₁' and 'M₂' designate the referent 'O'. The point 'O' is a referent which is an object. The point of the intersection between 'B' and 'C' designates 'O'. Thus M₁, M₂, and M₃ are the referring expressions and they designate the object called 'O'. So 'O' is the referent.

---

2	This graph has been taken from Munitz, M.K. (1981). Contemporary Analytic Philosophy. New York: Macmillan Publishing Co., INC, p.112, for the purpose of our own analysis.