Section IV: Sequence Circuits for Symmetrical Transmission Line
The schematic diagram of a transmission line is shown in Fig. 7.8. In this diagram the self impedance of the three phases are denoted by Zaa , Zbb and Zcc while that of the neutral wire is denoted by Znn . Let us assume that the self impedances of the conductors to be the same, i.e.,
Since the transmission line is assumed to be symmetric, we further assume that the mutual inductances between the conductors are the same and so are the mutual inductances between the conductors and the neutral, i.e.,
The directions of the currents flowing through the lines are indicated in Fig. 7.8 and the voltages between the different conductors are as indicated.
Fig. 7.8 Lumped parameter representation of a symmetrical transmission line.
Applying Kirchoff's voltage law we get
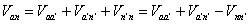
|
(7.41) |
Again
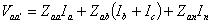
|
(7.42) |
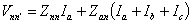
|
(7.43) |
Substituting (7.42) and (7.43) in (7.41) we get
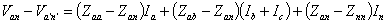
|
(7.44) |
Since the neutral provides a return path for the currents Ia , Ib and Ic , we can write
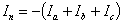
|
(7.45) |
Therefore substituting (7.45) in (7.44) we get the following equation for phase-a of the circuit
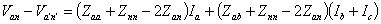
|
(7.46) |
Denoting
(7.46) can be rewritten as
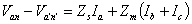
|
(7.47) |
Since (7.47) does not explicitly include the neutral conductor we can define the voltage drop across the phase-a conductor as
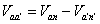
|
(7.48) |
Combining (7.47) and (7.48) we get
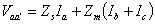
|
(7.49) |
Similar expression can also be written for the other two phases. We therefore get
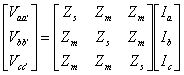
|
(7.50) |
Pre-multiplying both sides of (7.50) by the transformation matrix C we get
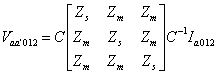
|
(7.51) |
Now
Hence
Therefore from (7.51) we get
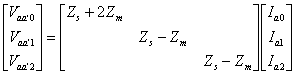
|
(7.52) |
The positive, negative and zero sequence equivalent circuits of the transmission line are shown in Fig. 7.9 where the sequence impedances are
Fig. 7.9 Sequence circuits of symmetrical transmission line: (a) positive, (b) negative and (c) zero sequence.
|