Section II: Sequence Circuits for Loads
In this section we shall construct sequence circuits for both Y and Δ -connected loads separately.
Sequence Circuit for a Y-Connected Load
Consider the balanced Y-connected load that is shown in Fig. 7.2. The neutral point (n) of the windings are grounded through an impedance Zn . The load in each phase is denoted by ZY . Let us consider phase-a of the load. The voltage between line and ground is denoted by Va , the line-to-neutral voltage is denoted by Van and voltage between the neutral and ground is denoted by Vn . The neutral current is then
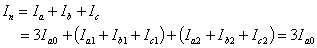
|
(7.22) |
Therefore there will not be any positive or negative sequence current flowing out of the neutral point.
Fig. 7.2 Schematic diagram of a balanced Y-connected load.
The voltage drop between the neutral and ground is
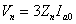
|
(7.23) |
Now
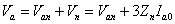
|
(7.24) |
We can write similar expression for the other two phases. We can therefore write
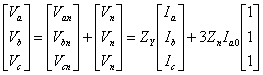
|
(7.25) |
Pre-multiplying both sides of the above equation by the matrix C and using (7.8) we get
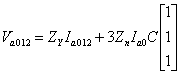
|
(7.26) |
Now since
We get from (7.26)
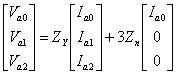
|
(7.27) |
We then find that the zero, positive and negative sequence voltages only depend on their respective sequence component currents. The sequence component equivalent circuits are shown in Fig. 7.3. While the positive and negative sequence impedances are both equal to ZY , the zero sequence impedance is equal to
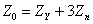
|
(7.28) |
If the neutral is grounded directly (i.e., Zn = 0), then Z0 = ZY . On the other hand, if the neutral is kept floating (i.e., Zn = ∞ ), then there will not be any zero sequence current flowing in the circuit at all.
Fig. 7.3 Sequence circuits of Y-connected load: (a) positive, (b) negative and (c) zero sequence.
|