Orthogonal Transformation
Instead of the transformation matrix given in (7.13), let us instead use the transformation matrix
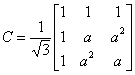
|
(7.19) |
We then have
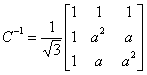
|
(7.20) |
Note from (7.19) and (7.20) that C -1 = ( CT )* . We can therefore state C( CT )* = I3 , where I3 is (3 × 3) identity matrix. Therefore the transformation matrices given in (7.19) and (7.20) are orthogonal. Now since
we can write from (7.17)
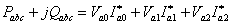
|
(7.21) |
We shall now discuss how different elements of a power system are represented in terms of their sequence components. In fact we shall show that each element is represented by three equivalent circuits, one for each symmetrical component sequence. |