Short Circuit in an Unloaded Synchronous Generator
Fig. 6.7 shows a typical response of the armature current when a three-phase symmetrical short circuit occurs at the terminals of an unloaded synchronous generator.
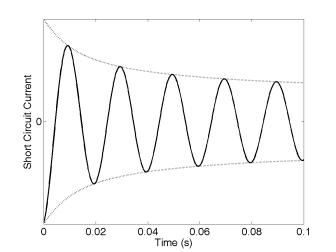
Fig. 6.7 Armature current of a synchronous generator as a short circuit occurs at its terminals.
It is assumed that there is no dc offset in the armature current. The magnitude of the current decreases exponentially from a high initial value. The instantaneous expression for the fault current is given by
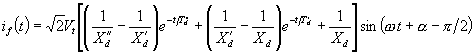 |
(6.9) |
where Vt is the magnitude of the terminal voltage, α is its phase angle and
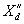 is the direct axis subtransient reactance is the direct axis subtransient reactance
|
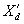 is the direct axis transient reactance is the direct axis transient reactance
|
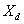 is the direct axis synchronous reactance is the direct axis synchronous reactance |
with 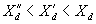 . The time constants are . The time constants are
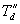 is the direct axis subtransient time constant is the direct axis subtransient time constant
|
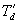 is the direct axis transient time constant is the direct axis transient time constant
|
In the expression of (6.9) we have neglected the effect of the armature resistance hence α = π/2. Let us assume that the fault occurs at time t = 0. From (6.9) we get the rms value of the current as
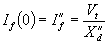 |
(6.10) |
which is called the subtransient fault current. The duration of the subtransient current is dictated by the time constant Td² . As the time progresses and Td² < t < Td¢ , the first exponential term of (6.9) will start decaying and will eventually vanish. However since t is still nearly equal to zero, we have the following rms value of the current
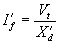 |
(6.11) |
This is called the transient fault current. Now as the time progress further and the second exponential term also decays, we get the following rms value of the current for the sinusoidal steady state
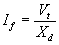 |
(6.12) |
In addition to the ac, the fault currents will also contain the dc offset. Note that a symmetrical fault occurs when three different phases are in three different locations in the ac cycle. Therefore the dc offsets in the three phases are different. The maximum value of the dc offset is given by
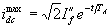 |
(6.13) |
where TA is the armature time constant.
|