Section V: Solution of a Set of Nonlinear Equations by Newton-Raphson Method
In this section we shall discuss the solution of a set of nonlinear equations through Newton-Raphson method. Let us consider that we have a set of n nonlinear equations of a total number of n variables x1 , x2 , ... , xn. Let these equations be given by
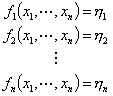 |
(4.22) |
where f1, ... , fn are functions of the variables x1 , x2 , ... , xn. We can then define another set of functions g1 , ... , gn as given below
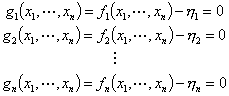 |
(4.23) |
Let us assume that the initial estimates of the n variables are x1(0) , x2(0) , ... , xn(0) . Let us add corrections Δx1(0) , Δx2(0) , ... , Δxn(0) to these variables such that we get the correct solution of these variables defined by
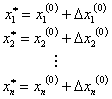 |
(4.24) |
The functions in (4.23) then can be written in terms of the variables given in (4.24) as
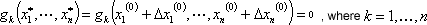 |
(4.25) |
We can then expand the above equation in Taylor 's series around the nominal values of x1(0) , x2(0) , ... , xn(0) . Neglecting the second and higher order terms of the series, the expansion of gk , k = 1, ... , n is given as
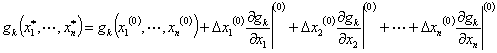 |
(4.26) |
where 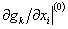 is the partial derivative of gk evaluated at x2(1) , ... , xn(1) . is the partial derivative of gk evaluated at x2(1) , ... , xn(1) .
Equation (4.26) can be written in vector-matrix form as
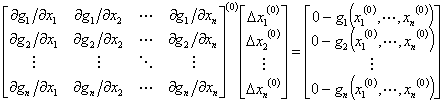 |
(4.27) |
The square matrix of partial derivatives is called the Jacobian matrix J with J (1) indicating that the matrix is evaluated for the initial values of x2(0) , ... , xn(0) . We can then write the solution of (4.27) as
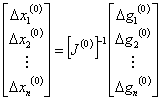 |
(4.28) |
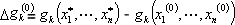 , k= 1, ....n , k= 1, ....n |
|
Since the Taylor 's series is truncated by neglecting the 2nd and higher order terms, we cannot expect to find the correct solution at the end of first iteration. We shall then have
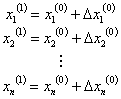 |
(4.29) |
These are then used to find J (1) and Δgk (1) , k = 1, ... , n . We can then find Δx2(1) , ... , Δxn(1) from an equation like (4.28) and subsequently calculate x2(1) , ... , xn(1). The process continues till Δgk , k = 1, ... , n becomes less than a small quantity.
|