Convergence of the Algorithm

As can be seen from Table 4.3 that a total number of 4 real and 3 reactive powers are known to us. We must then calculate each of these from (4.6) and (4.7) using the values of the voltage magnitudes and their angle obtained after each iteration. The power mismatches are then calculated from (4.9) and (4.10). The process is assumed to have converged when each of ΔP₂ , ΔP₃, ΔP₄ , ΔP₅ , ΔQ₂ , ΔQ₃ and ΔQ₄ is below a small pre-specified value. At this point the process is terminated.

Sometimes to accelerate computation in the P-Q buses the voltages obtained from (4.12) is multiplied by a constant. The voltage update of bus- i is then given by

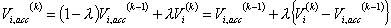(4.21)

where λ is a constant that is known as the acceleration factor . The value of λ has to be below 2.0 for the convergence to occur. Table 4.4 lists the values of the bus voltages after the 1^st iteration and number of iterations required for the algorithm to converge for different values of λ. It can be seen that the algorithm converges in the least number of iterations when λ is 1.4 and the maximum number of iterations are required when λ is 2. In fact the algorithm will start to diverge if larger values of acceleration factor are chosen. The system data after the convergence of the algorithm will be discussed later.

Table 4.4 Gauss-Seidel method: bus voltages after 1 st iteration and number of iterations required for convergence for different values of l .