Section IV:   Load Flow by Gauss-Seidel Method

• Updating Load Bus Voltages
• Updating P-V Bus Voltages
• Convergence of the Algorithm

The basic power flow equations (4.6) and (4.7) are nonlinear. In an n -bus power system, let the number of P-Q buses be n_p and the number of P-V (generator) buses be n_g such that n = n_p + n_g + 1. Both voltage magnitudes and angles of the P-Q buses and voltage angles of the P-V buses are unknown making a total number of 2n_p + n_g quantities to be determined. Amongst the known quantities are 2n_p numbers of real and reactive powers of the P-Q buses, 2n_g numbers of real powers and voltage magnitudes of the P-V buses and voltage magnitude and angle of the slack bus. Therefore there are sufficient numbers of known quantities to obtain a solution of the load flow problem. However, it is rather difficult to obtain a set of closed form equations from (4.6) and (4.7). We therefore have to resort to obtain iterative solutions of the load flow problem.

At the beginning of an iterative method, a set of values for the unknown quantities are chosen. These are then updated at each iteration. The process continues till errors between all the known and actual quantities reduce below a pre-specified value. In the Gauss-Seidel load flow we denote the initial voltage of the i ^th bus by V_i⁽⁰⁾ , i = 2, ... , n . This should read as the voltage of the i ^th bus at the 0^th iteration, or initial guess. Similarly this voltage after the first iteration will be denoted by V_i⁽¹⁾ . In this Gauss-Seidel load flow the load buses and voltage controlled buses are treated differently. However in both these type of buses we use the complex power equation given in (4.5) for updating the voltages. Knowing the real and reactive power injected at any bus we can expand (4.5) as

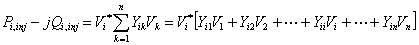(4.11)

We can rewrite (4.11) as

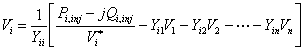(4.12)

In this fashion the voltages of all the buses are updated. We shall outline this procedure with the help of the system of Fig. 4.1, with the system data given in Tables 4.1 to 4.3. It is to be noted that the real and reactive powers are given respectively in MW and MVAr. However they are converted into per unit quantities where a base of 100 MVA is chosen.