Formation of the Jacobian Matrix

We shall now discuss the formation of the submatrices of the Jacobian matrix. To do that we shall use the real and reactive power equations of (4.6) and (4.7). Let us rewrite them with the help of (4.2) as

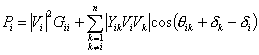
	(4.38)
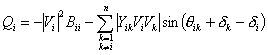	(4.39)

A. Formation of J₁₁

Let us define J₁₁ as

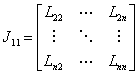(4.40)

It can be seen from (4.32) that L_ik's are the partial derivatives of P_i with respect to δ_k. The derivative P_i (4.38) with respect to k for i ≠ k is given by

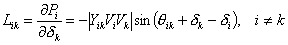(4.41)

Similarly the derivative P_i with respect to k for i = k is given by

Comparing the above equation with (4.39) we can write

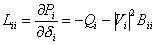(4.42)

B. Formation of J₂₁

Let us define J₂₁ as

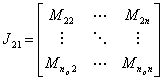(4.43)

From (4.34) it is evident that the elements of J₂₁ are the partial derivative of Q with respect to δ . From (4.39) we can write

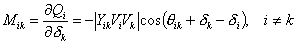(4.44)

Similarly for i = k we have

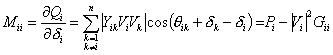(4.45)

The last equality of (4.45) is evident from (4.38).