Section II: Elements Of The Bus Impedance And Admittance Matrices

Equation (3.1) indicates that the bus impedance and admittance matrices are inverses of each other. Also since Y_bus is a symmetric matrix, Z_bus is also a symmetric matrix. Consider a 4-bus system for which the voltage-current relations are given in terms of the Y_bus matrix as

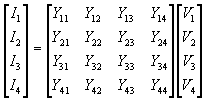(3.24)

We can then write

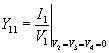(3.25)

This implies that Y₁₁ is the admittance measured at bus-1 when buses 2, 3 and 4 are short circuited. The admittance Y₁₁ is defined as the self admittance at bus-1. In a similar way the self admittances of buses 2, 3 and 4 can also be defined that are the diagonal elements of the Y_bus matrix. The off diagonal elements are denoted as the mutual admittances . For example the mutual admittance between buses 1 and 2 is defined as

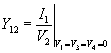(3.26)

The mutual admittance Y₁₂ is obtained as the ratio of the current injected in bus-1 to the voltage of bus-2 when buses 1, 3 and 4 are short circuited. This is obtained by applying a voltage at bus-2 while shorting the other three buses.

The voltage-current relation can be written in terms of the Z_bus matrix as

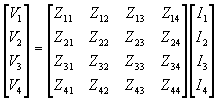(3.27)

The driving point impedance at bus-1 is then defined as

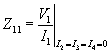(3.28)

i.e., the driving point impedance is obtained by injecting a current at bus-1 while keeping buses 2, 3 and 4 open-circuited. Comparing (3.26) and (3.28) we can conclude that Z₁₁ is not the reciprocal of Y₁₁ . The transfer impedance between buses 1 and 2 can be obtained by injecting a current at bus-2 while open-circuiting buses 1, 3 and 4 as

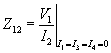(3.29)

It can also be seen that Z₁₂ is not the reciprocal of Y₁₂ .