Section I: Formation of Bus Admittance Matrix

• Node Elimination by Matrix Partitioning
• Node Elimination by Kron Reduction
• Inclusion of Line Charging Capacitors

Formation of Bus Admittance Matrix

Consider the voltage source V_S with a source (series) impedance of Z_S as shown in Fig. 3.1 (a). Using Norton's theorem this circuit can be replaced by a current source I_S with a parallel admittance of Y_S as shown in Fig. 3.1 (b). The relations between the original system and the Norton equivalent are

We shall use this Norton's theorem for the formulation of the Y_bus matrix.

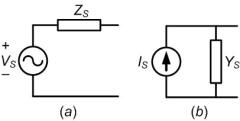
Fig. 3.1 (a) Voltage source with a source impedance and (b) its Norton equivalent.

For the time being we shall assume the short line approximation for the formulation of the bus admittance matrix. We shall thereafter relax this assumption and use the π -representation of the network for power flow studies. Consider the 4-bus power system shown in Fig. 3.2. This contains two generators G₁ and G₂ that are connected through transformers T₁ and T₂ to buses 1 and 2. Let us denote the synchronous reactances of G₁ and G₂ by X_G1 and X_G2 respectively and the leakage reactances of T₁ and T₂ by X_T1 and X_T2 respectively. Let Z_ij, i = 1, ..., 4 and j = 1, ... , 4 denote the line impedance between buses i and j .

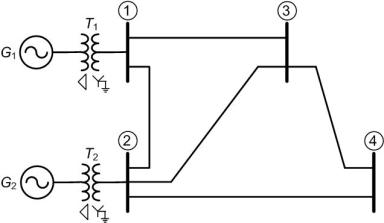
Fig. 3.2 Single-line diagram of a simple power network.