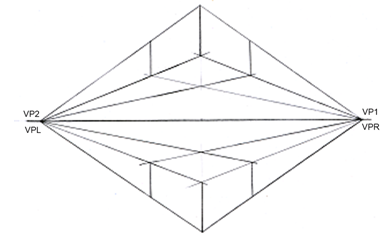
Fig.36(a): An example of two point perspective

Two-point Perspective:

Two-point perspective can be used to draw the same objects as one-point perspective, rotated: looking at the corner of a house, or looking at two forked roads shrink into the distance. For example, one point represents one set of parallel lines; the other point represents the other. Looking at a house from the corner, this refers as station point. (SP) one wall would recede towards one vanishing point, while the other wall would recede towards the opposite vanishing point. Two vanishing points (it usually refers to VP1 (right) and VP2 (left)) or VR and VL generated from the same horizon and define the contour of a particular object.

Two-point perspective has two sets of parallel line to the horizon and these two sets gradually converse to a vanishing point in the horizon, which has been already referred as VP1 and VP2. See fig. 36(a).

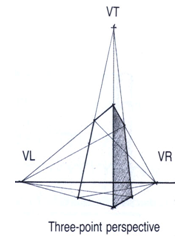
Fig.36(b) : An example of three point perspective

Three-point Perspective:

Three-point perspective is usually used for buildings seen from above (or below). In addition to the two vanishing points from before, one for each wall, there is a third to show how those walls recede into the ground. This third vanishing point will be below the ground. Looking up at a tall building is another common example of the third vanishing point. This time the third vanishing point is high in space.

Three-point perspective exists when the perspective is a view of a cartesian plane where the picture plane is not parallel to any of the scene's three axes. Each of the three vanishing points corresponds with one of the three axes of the scene.