In this method, precise time is being noted when the considered celestial body is being bisected. The observed time is used to derive the hour angle and declination of the celestial body at the instant of observation.
The geographic position (latitude and longitude) of the observation station is required to be known a priori for the hour angle method. Usually, these values are readily obtained from available maps. However, to achieve better accuracy, latitude and longitude must be more accurately determined specially during observations for celestial bodies close to the equator--e.g., the sun-than for bodies near the pole--e.g., Polaris.
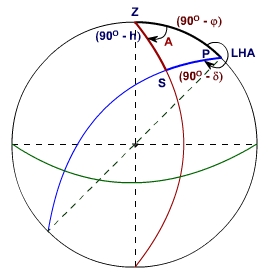
Figure 26.3 Astronomical Triangle
The declination of the celestial bodies at the instant of observation is required to be known for computation of azimuth of the celestial body. It is available in star almanac at the 0, 6, 12 and 18 hours of UTI of each day ( Greenwich date). Thus, the declination at the instant of observation (of celestial body) is determined by linear interpolation for corresponding the UT1 time of observation. However, since the declination of the sun varies rapidly, its interpolation is done using the relation:
Declination, d = Decl 0h + (Decl 24h - Decl 0h) ( ![]() ) + (0.0000395) (Decl 0h) sin (7.5 UT1) -------------(Equation 26.2)
) + (0.0000395) (Decl 0h) sin (7.5 UT1) -------------(Equation 26.2)
The hour-angle of the celestial body is being derived using the GHA (available in star almanac with reference to Greenwich date) and the longitude of the observation station. For observations in the Western Hemisphere, if UTI is greater than local time, the Greenwich date is the same as local date and if UTI is less than local time, Greenwich date is the local date plus one day. For the Eastern Hemisphere, if UTI is less than local time (24-hr basis), Greenwich date is the same as local date and if UTI is greater than local time, Greenwich date is local date minus one day. The hour angle of the celestial body at the observation station is the LHA. Thus, it is the LHA at UTI time of observation which is necessary to compute the azimuth of a celestial body. Hence, as can be seen from Figure 26.3, the equation for the LHA is
LHA = GHA - W l (west longitude) ----------------- (Equation 26.3)
Or LHA = GHA + E l (east longitude) -------------------(Equation 26.4)
LHA should be normalized to between 0° and 360° by adding or subtracting 360°, if necessary.
The Greenwich hour angle (GHA) of celestial bodies-the sun, Polaris, and selected stars-is tabulated in star almanac from 0 hr to 24 hr at an interval of 6 hours of UTI time of each day (Greenwich date). Thus, to find GHA at the time of observation linear interpolation is required to be performed.
The GHA can also be derived by making use of the equation of time E (apparent time minus mean time) by using the relation:
GHA = 180° + 15 E ---------------------------Equation (26.5)
where E is in decimal hours. In those cases where E is listed as mean time minus apparent time, the algebraic sign of E should be reversed.
Once the parameters (declination and Hour angle of the celestial body, latitude of the observation station) required to compute the azimuth of the celestial body are available, the computation of azimuth of the celestial body is carried out using the relations of astronomical triangle (Appendix- 25A).