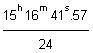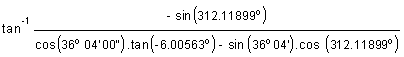Ex26-1 A celestial body is observed at a station (latitude 36° 04' 00" N and longitude 94° 10' 08" N). The UTI at the instant of observation was (15h 16m 41s.57).The GHA at 0hr (UT1) was found to be 177° 04 ' 44".1 on the day of observation and 177° 08' 06".3 on the next day. The declination of the selected body at 0hr (UT1) was + 6° 15' 05".9 S and + 5° 5' 54".7 S on the day of observation and next day respectively. Determine the azimuth of the celestial body.
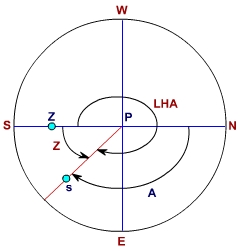
Figure Example 26.1
Soluton : Given, GHA at 0hr = 177° 04 ' 44".1
GHA at 24hr = 177° 08' 06".3
Instant of observation of the celestial body = 15h 16m 41s.57
Using linear interpolation method,
the GHA at the instant of observaton =
= 177° 04' 44".1 + (177° 08' 06".3 - 177° 04' 44".1 + 360°) x
= 406.28788° - 360° = 46.28788°
Thus,
Local Hour angle at the instant of observation, LHA = GHA - Wl (The station is at west to Greenwich)
= (46.28788° - 94° 10' 08") = - 47.88101° = -47.88101° + 360°
= 312.11899°
Declination (d)of the celestial body at the instant of observation (Implementing linear interpolation)
d = - 6° 15' 05".9 + ( - 5° 51' 54".7 + 6° 15' 05".9) x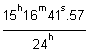 
= - 6.00563°
Now, using the relation (Equation 26.3), azimuth of the celestial body
Z =
=
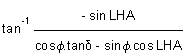
= - 57.10487745°
Since, LHA is between 180° and 360° and A is negative (Figure Ex 26.1), thus
Azimuth of the body, A = Z + 180° = - 57.10487745° + 180°
= 122.8951226° = 122° 53' 42 ".44