Ex40-1: A 200 meter equal tangent parabolic vertical curve is to be placed to negotiate a upward grade of 1.50% followed by a downward grade at 2.5% intersecting at a station having elevation 185.795 m above mean sea level. Calculate elevations at even 20 m stations on the vertical curve and determine the station and elevation of the highest point on the vertical curve.
Solution : Refer Figure Ex40-1(a)
The elevation of BVC = 185.795 - 0.015 x 100
= 184.295 m (above msl)
The elevation of EVC = 185.795 - 0.025 x 100
= 183.295 m (above msl)
From, the equation of parabola, the general equation of a vertical curve, is given by Equation (40.8)
in which, Y equals the elevation on the vertical curve at a distance X from BVC (Figure Ex40-1(a))
Given grade of first tangent, g1 = + 1.5% = + 0.015
grade of second tangent, g2 = - 2.5% = - 0.025
Length of the vertcal curve, L = 200 m
Substituting the given values, we get
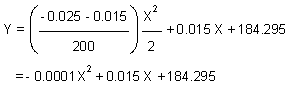
Table Ex.40-1 (a) Elevation of a vertical curve by Equation of Parabola (Figure Ex40-1 (a))
Table Ex. 40.1 (b) Elevation of points on vertical curve using vertical offset method (Figure Ex. 40.1(b))
Elevation of Tangent points (m)
[R.L. of BVC + g1x]
Vertical offset from Tangent (m)
The highest point is at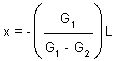 
, from equation (40.9)
Thus,
= 75 m from BVC
Therefore R.L. at the highest point,
Y = - 0.0001 (75)2 + 0.075 x (75) + 184.295
= - 0.5625 + 1.125 + 184.295 = 184.858 m