Consider a plane parabolic vertical curve AB of Figure 40.1 with the y axis passing through the BVC and the x axis corresponding to the datum for elevations. Let L be the length of the vertical curve in stations. The slope of the curve at the BVC is G1 and the slope at the EVC is G2. Since the rate of change in slope of a parabola is constant, the second derivative of y with respect to x is a constant, or
--------------- Equation (40.1)
Integration of Eq. (40.1) yields the first derivative or the slope of the parabola,
-------------------- Equation (40.2)
When x = 0, the slope =G1 and when x = L, the slope =G2. Thus,
G1 = 0 + H -------------------- Equation (40.3)
and G2 = r L + H -------------------- Equation (40.4)
Thus, from Equation (40.3) and Equation (40.4)
----------------- Equation (40.5)
The value of r is the rate of change of the slope in percent per station. Substitution of Eq.(40.5 and 40.3) into Eq.(40.2) gives
----------- Equation (40.6)
To obtain y, integrate Eq.(40.6) to yield
---------- Equation (40.7)
When x = 0, y is the elevation of the BVC and thus, c = elevation of the BVC or yBVC and Eq. (40.7) becomes
-------- Equation (40.8)
Which is the equation of the parabolic curve AB and can be used to calculate elevations of the curve given G1, G2, L, and the elevation of the BVC. Note that the first term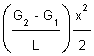 
, is the vertical offset between the curve and a point on the tangent to the curve at a distance x from the BVC. The second term G1 x represent the elevation on the tangent at a distance x from the BVC, and the third term is the elevation of the BVC above the datum.
Thus, reduced level at any point on a vertical at a distance x from starting station can be found by
The high or low point of a vertical curve is frequently of interest for drainage purposes. At the high or low point, the tangent to the vertical curve is zero. Equating the first derivative of y i.e., equation (40.6) to zero, provides
-------- Equation (40.9)