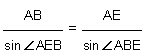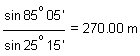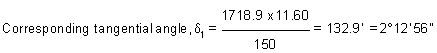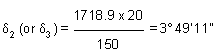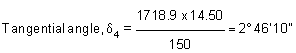Ex.38-1 A simple circular curve of radius 150m is to be set out between two straights, say AB and BC, having WCB 110° 20' and 85° 05'. The chainage of the starting point i.e., of A is 1252.00m. The coordinates of the starting and end points i.e., A and C are as follows
Point |
Coordinates (m) |
|
North |
East |
|
A |
201.64 |
62.20 |
C |
113.26 |
378.64 |
Compute the necessary data to set out the curve in field.
Solution :
Refer to Figure Example 38.1
The deflection angle, D at B = Bearing of AB - Bearing of BC
= 110° 20' - 85° 05' = 25° 15' (left)
In D ABE, REAB = 180° - 110° 20' = 69° 40'
REBA = Bearing of BA - Bearing of BE
= 290° 20' - 265° 05' = 25° 15'
RAEB = Bearing of BC = 85° 05'
Now, RECF = 270° - Bearing of CB
= 270° - (180° + 85° 05') = 4° 55'
Thus, EF = FC tan RECF
FC = Departure of C - Departure of A
= 378.64 - 62.20 = 316.44 m
EF = 316.44 tan 4° 55' = 27.22 m
Now, AF = Latitude of A - Latitude of C
= 210.61 - 113.26 = 88.38 m
Therefore, AE = AF + FE
= 88.38 + 27.22 = 115.6 m
Now, from D AEB
Or, AB = 115.6 x
(i) Lengths of tangent and curve
Let T1 and T2 be the first and second tangent point on AB and BC respectively, Then
tangent length BT1 = BT2 =
=
= 33.60m
Length of the curve, l =
=66.10m
(ii) Chainage of salient points
Given, chainage of A = 1252.00 m
Length of AB = 270.00
Therefore Chainage of B (point of intersection) = 1522m
Chainage of T1 = 1522 - BT1 = 1522 - 33.60 = 1488.40m
Chainage of T1 = Chainage of T1 + l
= 1488.40 + 66.10 = 1544.50m
(iii) Tangential Angles
The curve will set out with pegs at 20 m intervals. Thus, the curve is made up of four chords consisting of two normal chords and two sub-chords.
Length of the first sub-chord, C1 = 1500.00 - 1488.40 = 11.60 m
Length of 2nd and 3rd normal chords = 20 m. Then tangential angles, are
Length of last sub-chord, C4 = 1554.50 - 1540.00 = 14.50 m
The actual theodolite reading are considered assuming least count of theodolite = 10"
Check,
= 12° 37' 30" = deflection angles at point 3 (Verified)