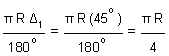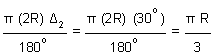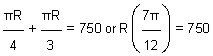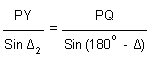WCB of the lines XY, ZY , AB are 45°, 300° and 90° respectively. The chainage of the station Y is 1000.00 m. A distance of 1 km is available for the curves alongwith the straight path. If the radius of the first curve is half of that of the second, calculate the following

• The radii of the curves
• The chainage of the point of tangencies

Solution :

Figure For Example 37.2

Solution :

(i) Deflection Angles

Deflection angle for the first curve

D₁ = Bearing of AB – Bearing of XY

= 90° – 45° = 45°

Deflection angle for the second curve

D₂ = Bearing of YZ – Bearing AB

= 120°– 90° = 30°

Deflection angle for the straights XY and YZ

D = D₁ + D₂ = 45° + 30° = 75°

D = Bearing of YZ - Bearing of XY = 120° - 45° = 75° (Verified)

(ii) Lengths of the Curves

Length of the first curve of radius R, say

l₁ =

Length of the second curve of radius, 2R

l₂ =

Total length of the curve, l = l₁ + l₂

(iii) Radius of the Curves

Given, Total length of the curves + straight path = 1000

or, l + 250 = 1000

or,

R = 409.26 m

Let us provide, the first curve having radius, R = 410.0 m

Thus, the radius of the second curve, 2R = 820.0 m

(iv) Tangent Length

Tangent length, T₁ P = R tan= 410 tan = 169.827 m = PA

Tangent length, T₂ Q = 2R tan = 820 tan = 219.717 m = QB

Thus, PQ = PA + AB + BQ

= 169.827 + 250 + 219.717 = 639.544 m

From D YPQ,

PY = x Sin 30° = 331.054 m

YT₁ = YP + PT₁ = 331.054+ 169.827 = 500.88 m

Let us provide YT₁ = 500 m;

(v) Chainage

Chainage of T₁ = Chainage of Y – YT₁

= 1000 – 500.00 = 500.00 m 

Chainage of A = Chainage of T₁ + l₁

= 500 + = 822.00 m

Chainage of B = Chainage of A + AB

= 822.00 + 250 = 1072.00 m

Chainage of T₂ = Chainage of B + l₂

= 1072.00 + = 1394.013 m

<< Back | Next >>