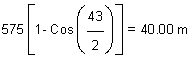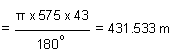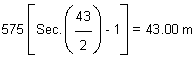Example 37.1 The deflection angle at the point of intersection (chainage 1256.260 m) of two straights is 43°. Find the elements of a 3° circular curve to be set out between the straights.
Solution Refer Figure 37.1
From Equation37.1, the radius of the circular curve,
R = 1718.9 / D = 1718.9 / 3 = 572.97 m ~ 573 m
Let us consider, the radius of the circular curve to be set be, R = 575 m
From given data,
the deflection angle, D = 43°
Thus, from Equation 37.2, tangent length T = R tan (D / 2) = 575 tan (43° / 2)
= 226.498 m = 226.50 m
Length of the curve, l =
(From Equation 37.1)
Chainage of T1 (the point of curve) = Chainage of P.I. – T
= 1256.260 – 226.50 = 1029.676 m
And Chainage of T2 (the point of tangency) = Chainage of P.C. + l
= 1029.76 + 431.533 = 1461.293 m
Length of the long chord, L = 2R Sin (D / 2) ------------------- (Equation 37.5)
= 2 x 575 x Sin (43° / 2) = 421.476 m
External distance, E =
------------------- (Equation 37.6)
=
Mid-ordinate distance, M = R (1 – Cos
) -------------------(Equation 37.7)
=