It should be noted here that q and K have the same dimension with the velocity. The value of q will be equal to K for unit hydraulic gradient. As such for the case of isotropic medium, the hydraulic conductivity (K) may be defined as the specific discharge (q) occurs under unit hydraulic gradient (J= 1).The hydraulic conductivity is dependent on both porous matrix properties and fluid properties and can be expressed as
|
(3.6) |
Where, ρ is the density of the fluid, µ is the viscosity of the fluid, v is the kinematic viscosity, k is the intrinsic permeability of the soil which depends on the properties of the porous matrix.
Considering (3.6), the Darcy’s Law can be written as
|
(3.7) |
It may be noted that in Darcy's law, we have neglected the kinetic energy of water. The velocity of water in case of porous medium is very low and along the flow path, the change in piezometric head is much smaller than the change in kinetic energy. Hence, kinetic energy can be neglected.
Further, it may be noted that the flow takes place from higher piezometric head to lower piezometric head and not from higher pressure to lower pressure. Only in case of horizontal flow (z1 = z2), the flow takes place from higher pressure to lower pressure. Thus incase of horizontal flow, the Darcy’s formula can be written as,
|
(3.8) |
Moreover, In case of flow through porous medium, the flow takes place only through the pores of the medium. Therefore, the cross sectional area through which the flow actually takes place is ηA. Where η is the porosity of the porous medium. As such, the average velocity of the flow can be expressed as
|
(3.9) |
Validity of Darcy’s Law
Darcy's law stated that the relation between specific discharge (q) and hydraulic gradient (J) is linear. However in real world situation, the relation becomes non-linear for higher values of specific discharge. As such, the Darcy’s law is not valid for higher specific discharge. The relation is generally linear as long as the Reynolds number does not exceed some value between 1 and 10. The Reynolds number, which is expressed as the ratio between inertial force and viscous force acting on the fluid, can be written as,
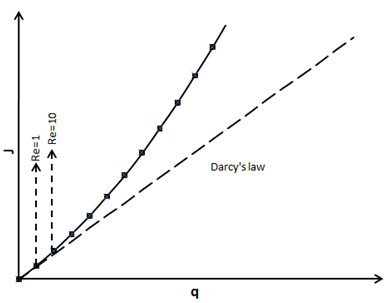 |
Fig. 2.3 Variation of specific discharge with hydraulic gradient |
|
(3.10) |
Where d is some representative length of the porous medium. It is often taken as the mean particle size of the porous medium. Sometime d10 is also taken as the representative length. d10 denotes the diameter at which 10 percent (by weight) of the soil grain size are smaller than that diameter. ϑ is the kinematic viscosity of the fluid. q is the specific discharge.
Darcy's law also stated that the flow is proportional to the hydraulic gradient. As per the law, if there is a small hydraulic gradient, there should have a very small specific discharge. However, in real situation there is a threshold value of hydraulic gradient. The flow will take place only when the hydraulic gradient is more than a threshold gradient. The threshold value of hydraulic gradient depends on the properties of porous matrix and properties of the fluid. For example, threshold value of the gradient may be high in case of clayey soil as the resistive force will be higher. The value of threshold gradient will also be high for the contaminated water which has higher viscosity than the uncontaminated water.