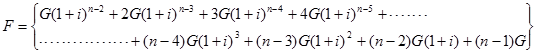(22)

Dividing both sides of equation (22) by (1+i)ⁿ results in the following equation;

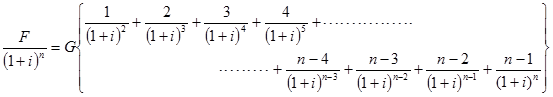(23)

Multiplying both sides of equation (23) by (1+i) results in the following expression;

(24)

Subtracting equation (23) from equation (24) results in the following expression;

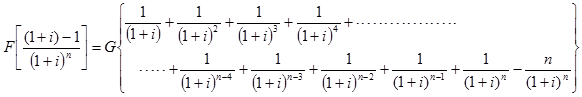(25)

The equation (25) can be rewritten as follows;

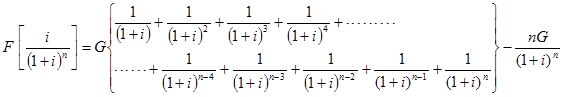(26)

The expression in the bracket is a geometric sequence with first term equal to 1/(1+i) and common ratio equal to 1/(1+i). Thus equation (26) is rewritten by taking sum of the first ‘n' terms of the geometric sequence (at i ≠ 0) and is given by;

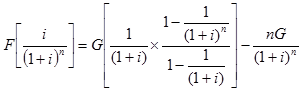(27)

The expression for future worth ‘F' can be written as follows:

(28)

The expression in the bracket is known as the uniform gradient future worth factor (UGFWF). With functional representation equation (28) can be rewritten as follows;

Thus the functional representation of uniform gradient future worth factor (UGFWF) can be written as follows;

(29)

It may be noted here that the future worth ‘F' occurs in the same year as that of the last gradient amount. Further the functional representations of other gradient factors can be found out by multiplying the relevant gradient factor with the compound interest factor at the given rate of interest ‘i' per interest period and number of interest periods ‘n'.